31. TLS

TLS (Transport Layer Security) is a protocol that provides an end-to-end encrypted communication channel. (You may sometimes see SSL, which is the old, deprecated version of TLS.) End-to-end encryption guarantees that even if any one part of the communication chain is compromised (for example, if the packet passes through a malicious AS), no one except the sender and receiver is able to read or modify the data being sent.

The original OSI 7-layer model did not consider security, so TLS is usually referred to as a layer 6.5 protocol. It is built on top of layer 4 TCP (layers 5 and 6 are obsolete), and it is used to provide secure communications to layer 7 applications. Examples of applications that use TLS are HTTP, which is renamed HTTPS if TLS is used; SMTP (Simple Mail Transport Protocol), which uses the STARTTLS command to enable TLS on emails; and VPN (Virtual Private Network) connections, which encrypt the user’s traffic.

TLS relies on TCP to guarantee that messages are delivered reliably in the proper order. From the application viewpoint, TLS is effectively just like a TCP connection with additional security guarantees.

31.1. TLS Handshake

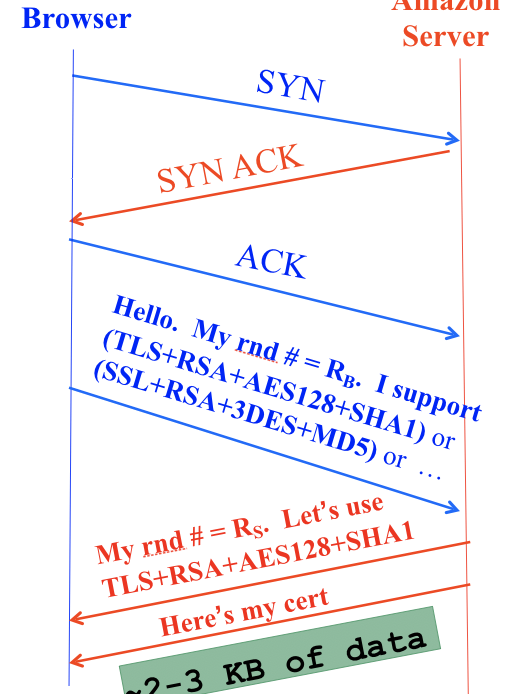
Because it’s built on top of TCP, the TLS handshake starts with a TCP handshake. This lets us abstract away the notion of best-effort, fixed-size packets and think in terms of reliable messages for the rest of the TLS protocol.

The first message, ClientHello, presents a random number \(R_B\) and a list of encryption protocols it supports. The client can optionally also send the name of the server it actually wants to contact.

The second message, ServerHello, replies with its own random number \(R_S\), the selected encryption protocol, and the server’s certificate, which contains a copy of the server’s public key signed by a certificate authority (CA).

If the client trusts the CA signing the certificate (e.g. that CA is included in the Chrome browser’s pinned list of trusted CAs), then the client can use the signature to verify the server’s public key is correct. If the client doesn’t directly trust the CA, it may need to verify a chain of certificates in a PKI until it reaches the trusted root of the certificate chain. Either way, the client now has a trusted copy of the server’s public key.

What is the public key being sent here? Every server implementing TLS must maintain a public/private key pair in order to support the PS exchange step you’ll see next. We will assume that only the server knows the private key - if an attacker steals the private key, they would be able to impersonate the server, and the security guarantees no longer hold.

Sanity check: After the first two messages, can the client be certain that it is talking to the genuine server and not an impostor?¹

The next step in TLS is to generate a random Premaster Secret (PS) known to only the client and the server. The PS should be generated so that no eavesdropper can determine the PS based on the data sent over the connection, and no one except the client and the legitimate server have enough information to derive the PS.

The first way to derive a shared PS is to encrypt it with RSA, shown in the last (blue) arrow here that depicts \(\{PS\}_{K_{server}}\):

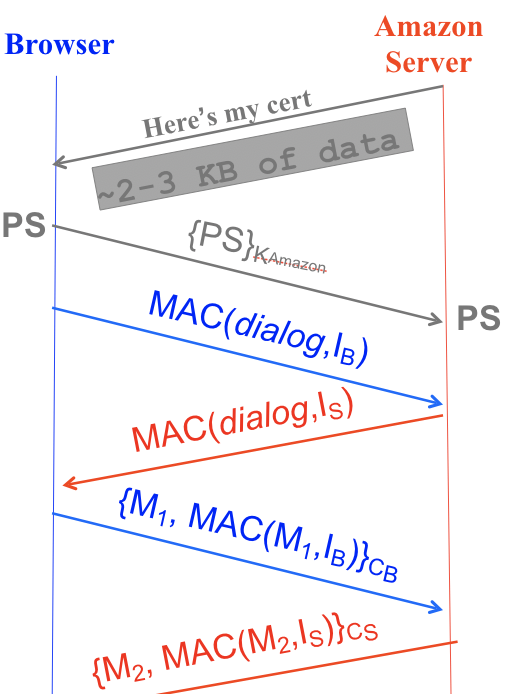
Here, the client generates the random PS, encrypts it with the server’s public key, and sends it to the server, which decrypts using its private key.

Sanity check: How can the client be sure it’s using the correct public key?²

We can verify that this method satisfies all the properties of a PS. Because it is encrypted when sent across the channel, no eavesdropper can decrypt and figure out its value. Also, only the legitimate server will be able to decrypt the PS (using its secret key), so only the client and the legitimate server will know the value of the PS.

The second way to generate a PS is to use Diffie-Hellman key exchange, shown in the fourth (red) and fifth (blue) arrows here that depict \(\{g^a \bmod p\}_{K^{-1}_{server}}\) and \(g^b \bmod p\) respectively:

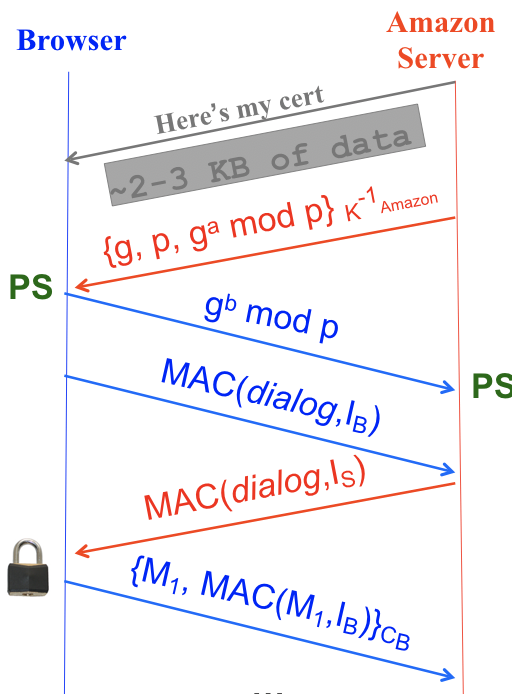
The exchange looks just like classic Diffie-Hellman, except the server signs its half of the exchange with its secret key. The shared PS is the result of the key exchange, \(g^{ab} \bmod p\).

Again, we can verify that this satisfies the properties of a PS. Diffie-Hellman’s security properties guarantee that eavesdroppers cannot figure out PS, and no one but the client and the server know PS. We can be sure that the server is legitimate because the server’s half of the key exchange is signed with its secret key.

An alternate implementation here is to use Elliptic Curve Diffie-Hellman (ECDHE). The specifics are out of scope, but it provides the same guarantees as regular DHE using elliptic curve math.

Generating the PS with DHE and ECDHE has a substantial advantage over RSA key exchange, because it provides forward secrecy. Suppose an attacker records lots of RSA-based TLS communications, and some time in the future manages to steal the server’s private key. Now the attacker can decrypt PS values sent in old connections, which violates the security of those old TLS connections.

On the other hand, if the attacker steals the private key of a server using DHE or ECDHE-based TLS, they have no way of discovering the PS values of old connections, because the secrets required to generate the PS (\(a\), \(b\)) cannot be discovered using the data sent over the connection (\(g^a, g^b \bmod p\)). Starting from TLS 1.3, RSA key exchanges are no longer allowed for this reason.

Now that both client and server have a shared PS, they will each use the PS and the random values \(R_B\) and \(R_S\) to derive a set of four shared symmetric keys: an encryption key \(C_B\) and an integrity key \(I_B\) for the client, and an encryption key \(C_S\) and an integrity key \(I_S\) for the server.

Up until now, every message has been sent in plaintext over TLS. Sanity check: how might this be vulnerable?³

In order to ensure no one has tampered with the messages sent in the handshake so far, the client and server exchange and verify MACs over all messages sent so far. Notice that the client uses its own integrity key \(I_B\) to MAC the message, and the server uses its own integrity key \(I_S\). However, both client and server know the value of \(I_B\) and \(I_S\) so that they can verify each other’s MACs.

At the end of a proper TLS handshake, we have several security guarantees. (Sanity check: where in the handshake did these guarantees come from?)

1. The client is talking to the legitimate server.

2. No one has tampered with the handshake.

3. The client and server share a set of symmetric keys, unique to this connection, that no one else knows.

Once the handshake is complete, messages are encrypted and MAC’d with the encryption and integrity keys of the sender before being sent. Because these messages have full confidentiality and integrity, TLS has achieved end-to-end security between the client and the server.

31.2. Replay attacks

Recall that a replay attack involves an attacker recording old messages and sending them to the server. Even though the attacker doesn’t know what these messages decrypt to, if the protocol doesn’t properly defend against replay attacks, the server might accept these messages as valid and allow the attacker to spoof a connection.

The public values \(R_B\) and \(R_S\) at the start of the handshake defend against replay attacks. To see why, let’s assume that \(R_B = R_S = 0\) every time and try to execute a replay attack on RSA-based TLS. Since the attacker is sending the same encrypted PS, and \(R_B\) and \(R_S\) are not changing, the server will re-generate the same symmetric keys. Now the attacker can replay messages from the old TLS connection, which will be accepted by the server because they have the correct MACs. Using new, randomly generated values \(R_B\) and \(R_S\) every time ensures that each connection results in a different set of symmetric keys, so replay attacks trying to establish a new connection with the same keys will fail.

What about a replay attack within the same connection? In practice, messages sent over TLS usually include some counter or timestamp so that an attacker cannot record a TLS message and send it again within the same connection.

31.3. TLS in practice

The biggest advantage and problem of TLS is the certificate authorities. “Trust does not scale”, that is, you personally can’t make trust decisions about everyone, but trust can be delegated, which is how TLS operates. We have delegated to a large number of companies, the Certificate Authorities, the responsibility of proving that a particular public key can speak for a particular site. This is what allows the system to work at all. But at the same time, unless additional measures are taken, this means that all CAs need to be trusted to speak for every site. This is why Chrome, for example, has a “pinned" CA list, so only some CAs are allowed to speak for certain websites.

Similarly, newer CAs implement certificate transparency, a mechanism where anyone can see all the certificates the CA has issued, implemented as a hash chain. Such CAs may issue a certificate incorrectly, but the impersonated victim can at least know this has happened. Certificates also expire and can be revoked, where a list of no-longer accepted certificates is published and regularly downloaded by a web browser or an online-service provides a mechanism to check if a particular certificate is revoked.

These days TLS is effectively free. The computational overhead is minor to the point of trivial: an ECDSA signature and ECDHE key exchange for the server, and such signatures and key exchanges are computationally minor: a single modern processor core can do tens of thousands of signatures or key exchanges per second. And once the key exchange is completed the bulk encryption is nearly free as most processors include routines specifically designed to accelerate AES.

This leaves the biggest cost of TLS in managing the private keys. Previously CAs charged a substantial amount to issue a certificate, but LetsEncrypt costs nothing because they have fully automated the process. You run a small program on your web server that generates keys, sends the public key to LetsEncrypt, and LetsEncrypt instructs that you put a particular file in a particular location on your server, acting to prove that you control the server. So LetsEncrypt has reduced the cost in two ways: It makes the TLS certificate monetarily free and, as important, makes it very easy to generate and use.

Past Exam Questions

Here we’ve compiled a list of past exam questions that cover TLS.

• Spring 2024 Final Question 9: Key Rotation
• Fall 2023 Final Question 11: New Phone Who This
• Spring 2023 Final Question 9: TLS Times Two

1. A: No. An attacker can obtain the genuine server’s certificate by starting its own TLS connection with the genuine server, and then present a copy of that certificate in step 2. ↩

2. A: It was signed by a certificate authority in the previous step. ↩

3. A: TCP is insecure against on-path and MITM attackers, who can spoof messages. ↩